|
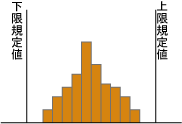
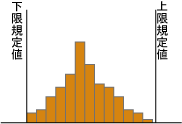
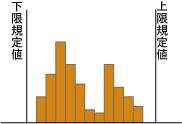
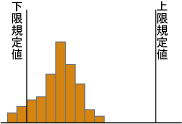
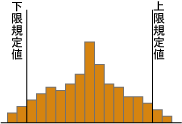
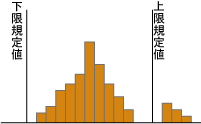
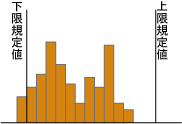
次に示すヒストグラムの見方と処置について最も適当なものはどれか。 |
|
 |
|
| 1 |
下限規格値をはずれている原因を調べる。 |
| 2 |
品質特性値を高い方に寄せる。 |
| 3 |
層別して原因を調べる必要がある。 |
| 4 |
品質標準を改める。 |
|
解答 (3)
下限規格値をはずれているものがあり,また分布の山が二つあることが問題である。データを材料別,ロット別,時間別等に層別して原因を調べる。また特性値を高い方に上げるように工程を改善する。
|
| 規格値に対するゆとり |
 |
品質管理において,下限規格値を12kgf/c㎡と定めて施エした現場から得た測定値の平均は,20kgf/c㎡,標準偏差の推定値は2 kgf/c㎡であった。この結果からの判定で適当なものはどれか。 |
|
| 1 |
規格値に対してゆとりがない。 |
| 2 |
規格値すれすれのものもあり変動に注意を要する。 |
| 3 |
規格値からはずれるものもあり調査を要する。 |
| 4 |
規格値に対して十分ゆとりがある。 |
|
解答 (4)
片側(上限又は下限)規格の場合のゆとりの判定は,次式で3以上とする。
(上限(又は下限)限界値-平均値)/標準偏差=(12-20)/2=4 ≧3 OK
|
| 工程能カ図 |
 |
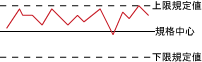
下記の工程能カ図の説明に関して適当でないものはどれか。 |
|
|
|
| 1 |
①図は,上限規格値を外れているものがあり,全体を下げる。 |
| 2 |
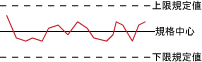
②図は,規格内におさまっているが,バラツキが大きく不安定である。 |
| 3 |
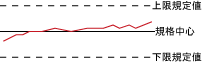
③図は,点が中心線に近く,しかも変動幅が小さく安定している。 |
| 4 |
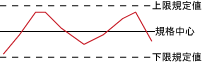
④図は,周期的な変動を示しており,安定状態とはいえない。 |
|
解答 (3)
一定の方向で徐々に上昇しているのは異常な場合あり。品質が時間の経過などにより変化している可能性もある。

|
| 解説 |
| ヒストグラム |
| 1 |
ヒストグラムとは,横幅に品質特性値のバラツキを一定幅のクラスに分け,縦幅に各クラスの度数を柱状図に表わしたもの。 |
| 2 |
品質の規格値を記入することにより,規格値とゆとりの関係も明確となる。 |
| 3 |
図のヒストグラムの判定は次のとおり。 |
|
|
|
| ① |
規格値もバラツキもよく,ゆとりもあり,平均値が規格の中央にあり良。 |
| ② |
規格値すれすれのものもあり,将来少しの変動でも規格を割るものができる可能性がある。バラツキに注意を要する。 |
| ③ |
山が二つあり工程に異常が起こっている。他の母集団のものが入っていることも考えられ,全部のデータをもう一度調べる必要がある。 |
| ④ |
下限規格値を割るものがあり,平均値を大きい方にずらす処置が必要。 |
| ⑤ |
下限規格値も上限規格値も割っており,何らかの処置が必要である。現状の技術レペル又は作業標準等に問題はないか,検討を要する。 |
| ⑥ |
大部分が規格の幅のいっぱいにバラツキ,右の方に離れ小島がある。要検討。 |
|
|
| 品質特性(管理項目)を決定するに当っては,次の点に注意する。 |
| ① |
工程の状態を総合的に表わすもの。 |
| ② |
代用特性が明確なもの(真の特性で検査できない場合)。 |
| ③ |
設計品質(最終品質)に重要な影響を及ぼすもの。 |
| ④ |
測定し易いもの。 |
| ⑤ |
工程に対して処置のとり易いもの。 |
|
| 工程能カ図 |
| 1 |
横軸にサンプル番号又は時間,縦軸に特性値を取り,規格中心値,上下規格値を示す線を引き,データを打点し,時間的な品質の変動を知る。 |
| 2 |
管理図と形は似ているが,統計的な処理はなく,規格はずれ,点の並び方からヒストグラムでは分からない品質特性値の時間的変化・傾向を知る。 |
|
|
|
|
|